Path Planning for Autonomous Vehicles in Unknown Semi-structured Environments
本文为其姊妹篇会议论文(Practical Search Techniques in Path Planning for Autonomous Driving)的扩展,时隔一年发表在机器人顶刊 IJRR 上,内容无太大变化。
算法分为两步:
- A* 搜索的变体,结合车辆动力学,进行路径搜索;
- 数值非线性优化提升解的质量,新增结合先验信息模块;
1 Introduction
- 主要难点:
- 连续变量的优化;
- 时间成本
- 非结构化环境
2 Hybrid-state A* Search
- 算法描述:
- 自车起始状态:
- 目标状态:
- 扩展的4D状态空间:
, 是自车的行进方向,前进or后退 - 惩罚倒车(乘性惩罚)和切换行驶方向(加性惩罚)的行为。
- 自车起始状态:
- 本文没有速度规划,使用固定的 5 mph 速度
- 节点从open list中pop out,根据运动学连接三个节点:最大左转,直行,最大右转,hybrid A*生成的轨迹一定是可达的,但不保证全局最优。
Heuristics
- 使用了两个启发式函数:
non-holonomic-without-obstacles heuristic, 忽略障碍物,但考虑到汽车的非完整性。holonomic-with-obstacles heuristic,与上一个启函数对称,忽略汽车的非完整约束,考虑障碍物地图计算最短路径。
- During the Urban Challenge, we used a 160 m X 160 m grid with 1 m X 5 deg resolution.
- 用 Reed–Shepp model 优化hybrid A*的解,计算最优的 Reed–Shepp path
- Reeds, J. A. and Shepp, L. A. (1990). Optimal paths for a car that goes both forwards and backwards. Pacific Journal of Mathematics, 145(2): 367–393.
- 变分辨率搜索(Variable Resolution
Search),计算中期望竟可能精细的分辨率,主要原因在于:
- 完整性,分辨率太粗,狭窄的通道不能通过;
- 最优性,粗分辨率导致轨迹在最优解附近震荡了;
- 计算效率;
- 具体实施:在宽阔的地方使用大步长,在狭窄的地方使用小步长;利用Generalized
Voronoi Diagram (GVD)中的
变化规划的弧长长度,实现变分辨率, 是最近障碍物距离, 是GVD最近边界的距离;
3 Trajectory Optimization
- 计算流程:
- Hybrid A*(0.5-1m)
- R-S曲线(0.5-1m)
- 共轭梯度轨迹平滑(0.5-1m)
- 非参数插值(5-10cm)
- 共轭梯度轨迹平滑(5-10cm)
Trajectory Smoothing via Conjugate Gradient
- 该步骤同之前的文章,此处不再描述;
Guaranteeing Smoother Safety
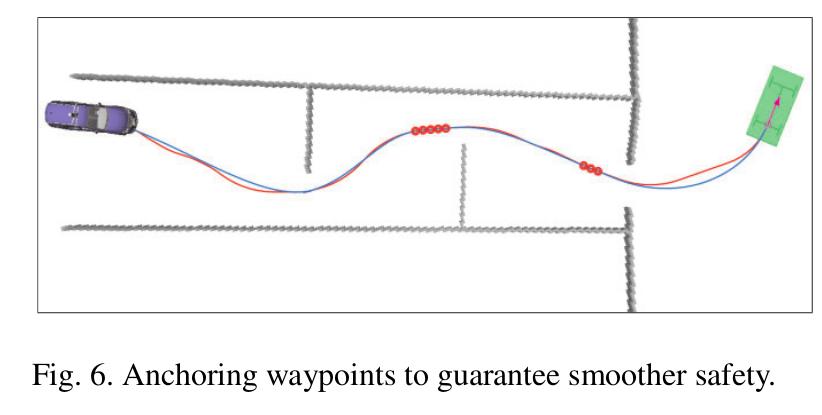
- 共轭梯度轨迹平滑中虽然加了碰撞惩罚,但是并不能保证无碰撞,优化目标也没考虑车身形状,因此不能精确优化轨迹。如果在共轭梯度轨迹平滑模块内实施精确的碰撞检测,那么计算量又会过大;
- 共轭梯度法平滑的轨迹如果不安全,则锚定住A* solution中的相关点。迭代优化其余点,直到collision-free
Navigation Potential Using the Voronoi Field
- 使用了Voronoi Field得到导航信息,这部分和之前论文一样,不重复介绍。
4 Graph-guided Path Planning in Semi-structured Environments
Trajectory Smoothing in Semi-structured Environments
本文增加了这部分内容,在GC优化项中增加了一项。感觉意义不是太大,这里不再介绍。
总结
本文和之前的会议论文差不多,感觉意义新加部分意义不是很大。