Practical Search Techniques in Path Planning for Autonomous Driving
本文是stanford大学在 2007 DARPA Urban Challenge 中产出的一项工作,提出了著名的混合A*算法。
混合A*算法包含两个主要步骤:
- 求解基于改进的A*算法的粗略轨迹,节点之间在动力学上是连续的;
- 使用数值非线性优化提升轨迹质量;
1 Introduction
- 结合 rapidly exploring random trees (RRTs)
的连续路径规划算法,但他们依赖高效的启发式引导:
- Kavraki, L.; Svestka, P.; Latombe, J.-C.; and Overmars, M. 1996. Probabilistic roadmaps for path planning in high-dimensional configuration spaces. IEEE Transactions on Robotics and Automation 12(4).
- LaValle, S. 1998. Rapidly-exploring random trees: A new tool for path planning.
- Plaku, E.; Kavraki, L.; and Vardi, M. 2007. Discrete search leading continuous exploration for kinodynamic motion planning. In Robotics: Science and Systems.
- 步骤:
- step 1:使用启发式搜索在连续的坐标空间中规划满足动力学的轨迹。但该方法缺少理论上的最优保证;
- step 2:使用共轭梯度(conjugate gradient, CG)下降来局部改善解的质量,产生至少是局部最优的路径,但通常也达到全局最优。
2 Hybrid-State A* Search
- 本文的方法的第一阶段使用3D运动学状态空间的
算法的变体,但修改了状态更新规则,该规则在 的离散搜索节点中使用连续状态。 - 由于合并了同一网格中的连续坐标状态,因此不保证损失最小解(minimal-cost solution),但路径一定是可行的(drivable)。
- 搜索空间
,每个状态节点之间是动力学连续的。但是搜索过程中转向角是离散化的,考虑离散化和精度之间的关系,使用 Reed-Shepp model 进行轨迹扩展 (We used a 160x160 grid with 1m resolution in x-y and 5 deg angular resolution.) - Reeds, J. A., and Shepp, L. A. 1990. Optimal paths for a car that goes both forwards and backwards. Pacific Journal of Mathematics 145(2):367–393
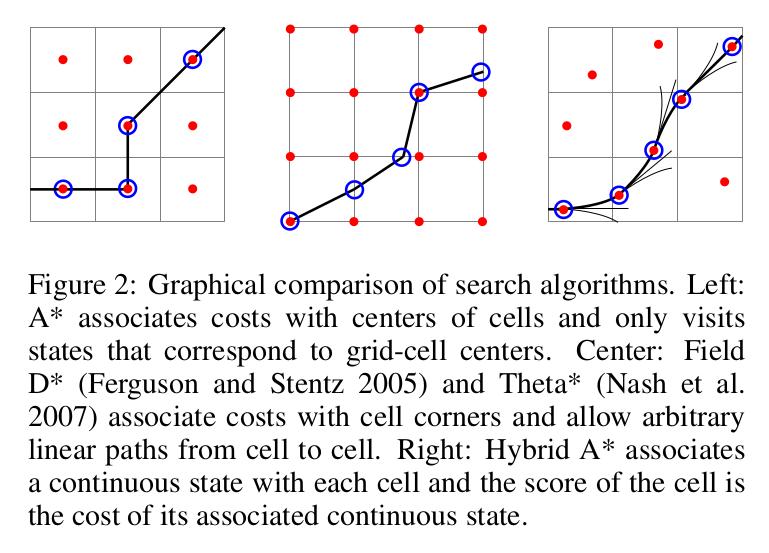
- 算法规划向前和向后的运动,并对向后驾驶以及转换运动方向进行惩罚
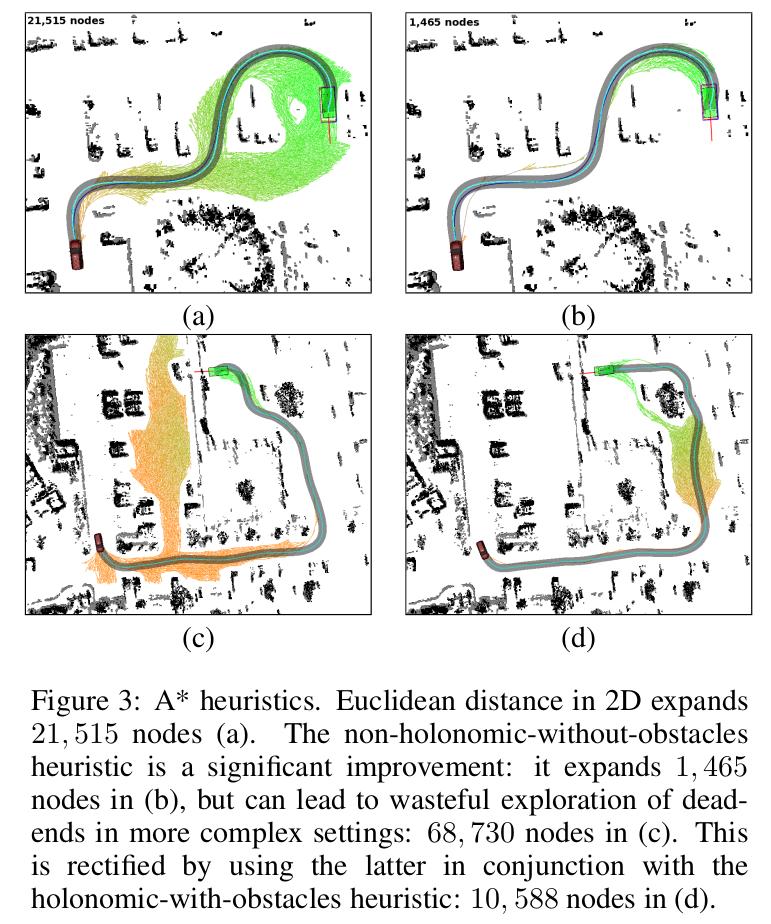
- 两个启发式步骤:
- “non-holonomic-without-obstacles” ,忽略障碍物,但考虑到汽车的非完整性,计算目标点邻域内到该点的最短路径
- 考虑障碍物和动力学,计算到目标的最短距离,其优势在于可以发现2D地图所有的U形障碍和死胡同,引导更代价昂贵的3D搜索远离这些区域。
- 对求解的 Reed-and-Shepp path 进行碰撞检测,确定无碰撞后才会加入到路径树中。
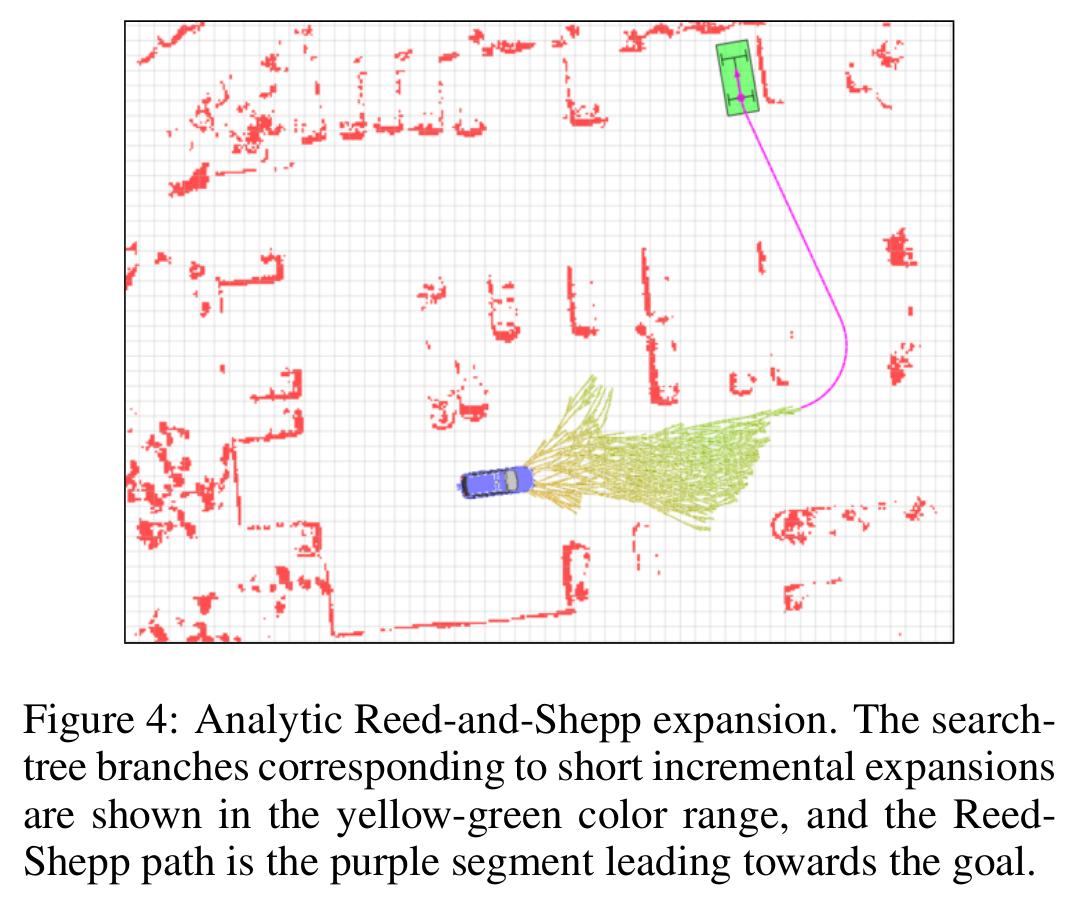
- 出于计算的原因,不希望将Reed-Shepp展开应用于每个节点(尤其是远离目标的节点,在那里大多数这样的路径可能会穿过障碍物)。在我们的实现中,我们使用了一个简单的选择规则,其中Reed-Shepp扩展应用于每N个节点中的一个,其中N作为目标成本启发式算法的函数而减少(随着我们越来越接近目标,导致更频繁的分析扩展)。
- 带有Reed-Shepp扩展的搜索树如下图所示。由节点的短增量扩展生成的搜索树显示在黄绿色范围内,Reed-Shepp扩展显示为通向目标的单紫色线。我们发现,搜索树的这种分析扩展在准确性和计划时间方面都带来了显著的好处。
3 Path-Cost Function Using the Voronoi Field
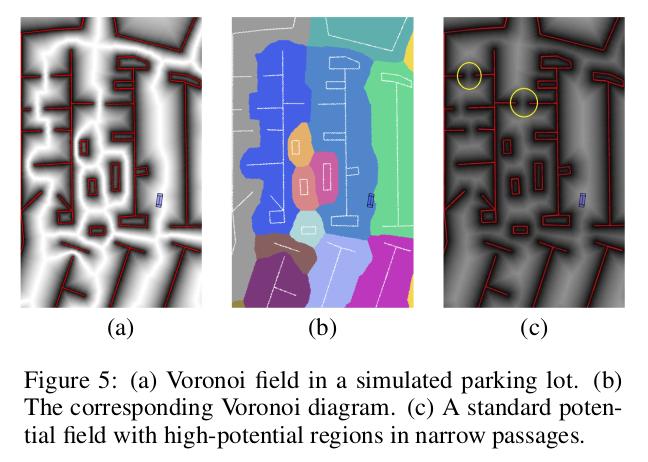
- 使用流动势场法(following potential field)权衡路径长度和与障碍物的距离,将其命名为Voronoi Field
表达式满足
- 势场有以下几个原则:
时其值为0; ,并且在 处连续,因为不存在同时满足 的情况; - 势场仅在障碍物内部取到最大值;
- 势场仅在GVD边界上取到最小值;
- Voronoi场比传统势场的关键优势在于,场值与导航的可用间隙成比例。即使狭窄的开口仍然可以通航,而标准势场并不总是如此,传统势场可能封闭这些道路。
4 Local Optimization and Smoothing
- hybrid-state A* 产生的轨迹仍然是次优的,需要进一步优化,去除不自然的突然转弯(unnatural swerves)。
- 优化过程分为两步:
- 对轨迹的每个顶点使用非线性优化平滑
- 对轨迹进行非参数的插值(non-parametric interpolation),使用共轭梯度提升轨迹分辨率。
- 变量定义:
表示顶点序列; 表示离顶点最近的障碍物坐标; 表示顶点的位移矢量; 表示顶点处的切角变化;
- 目标函数定义为:

损失函数的第一项可以高效地引导机器人移动,无论狭窄和开阔的地方都能远离障碍物;
第二项惩罚与障碍物的碰撞;
第三项限制每个顶点处的瞬时曲率,并加强车辆的非完整约束;
第四项是路径平滑措施;
- 梯度求解:



- 经过共轭梯度法的优化,轨迹显著更平滑了,但顶点之间仍有较大间距(论文中0.5-1m)。因此需要对轨迹进行再次插值。但许多参数化的插值算法对噪声敏感,加剧输出中的噪声(例如,随着输入顶点彼此靠近,三次样条曲线会导致输出中包含任意大的振荡)。
- 本文对共轭梯度法轨迹进行了非参数化的插值,之后再用共轭梯度法进行平滑
- We used the following parameters for our planner: the obstacle map was of size 160m×160m with 0.15cm resolution; A* used a grid of size 160m×160m×360◦ with 0.5m x-y resolution and 5◦ resolution for the heading θ. Typical running times for a full replanning cycle involving the hybrid A* search, CG smoothing, and interpolation were on the order of 50–300ms.

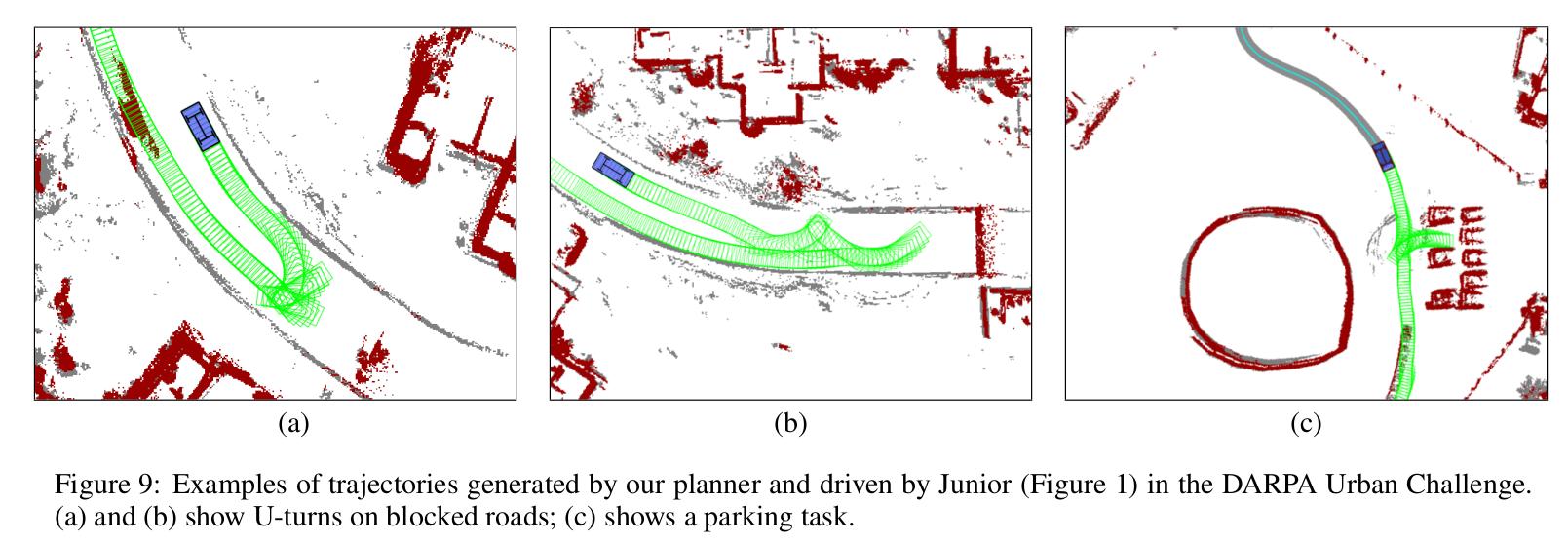
总结
本文面向AVP问题,发表于2008年,整体思路很清晰:hybird A*求粗略轨迹->共轭梯度轨迹平滑->非参数插值->共轭梯度轨迹平滑。方法受年代限制,没有使用NN优化,这或许是一个可以产生明显提升的地方